

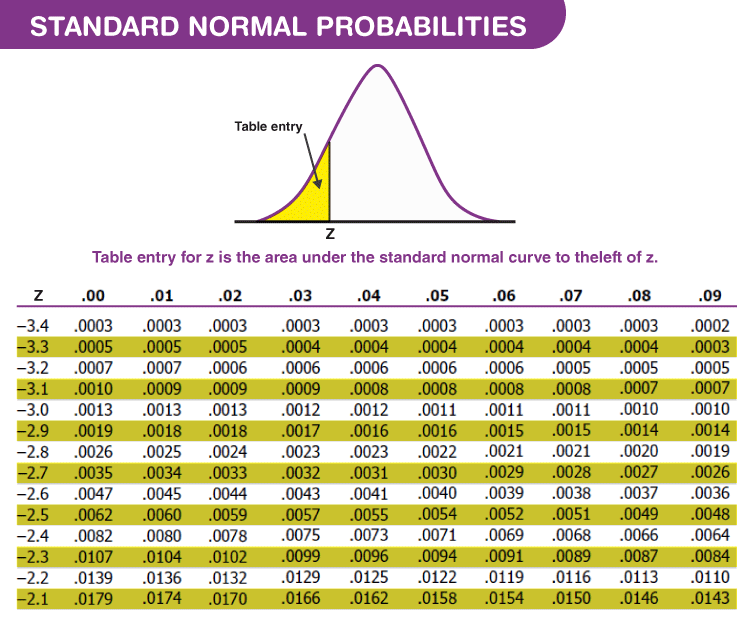
Suppose you perform a repetitive task that can be described by the normal distribution (such as a production of a standardized good) in the long run. Such events may be considered as very unlikely: accidents and mishaps, on the one hand, and streaks of luck, on the other. If this principle is successfully applied, you can expect to have 3.4 defects for every one million realizations of a process. If you try to expand this interval and go six sigmas to the left and right, you will find out that 99.9999998027% of your data points fall into this principle. Hence, only 0.3% of this process's possible realizations will lay outside of the three sigma interval. To learn more about this quantity, head to Omni's p-value calculator.ĩ9.7% of observations of a process that follows the normal distribution can be found either to the right or to the left from the distribution mean. Knowing this area, you can also find the p-value - the probability that the score will be higher than 62. Hence, we can say that the probability of a student scoring 62 or lower on the test is equal to 0.6591, or 65.91%. Remember that the total area under this graph is equal to 1. The area under the standard distribution graph (to the left of our z-score) is equal to 0.6591. It will determine the row in which you must look. Then, find the value of 0.01 in the first row. First, you need to find z = 0.4 in the first column this value shows you in which row you need to seek. In the first row, you can find the digit that is in the second decimal place of your z-score.įor example, we found the z-score of 62 in our example to be equal to 0.41. The first column of the table is a list of z-values (accurate to one decimal place). A z-score table is where you can find the area to the left of the given z-score under the standard distribution graph.


 0 kommentar(er)
0 kommentar(er)
